Bio
“Countdown to a Cure? Mathematical Approaches to Designing Better HIV Treatments”
Dr. Alison Hill is a Research Fellow and independent principle investigator at Harvard University’s Program for Evolutionary Dynamics. She holds a NIH Director’s Early Independence Award and is a member of the John Harvard Distinguished Science Fellows program. Dr. Hill develops mathematical and computational tools to help better understand, predict, and treat infectious diseases, with a particular focus on human viral infections including HIV/AIDS. Hill received her PhD in 2013 through Harvard’s Biophysics Program and was a joint graduate student in the Harvard-MIT Division of Health-Sciences and Technology (HST)’s Medical Engineering and Medical Physics program. She received her undergraduate degree in Physics from Queen’s University in Ontario, Canada.
is a Research Fellow and independent principle investigator at Harvard University’s Program for Evolutionary Dynamics. She holds a NIH Director’s Early Independence Award and is a member of the John Harvard Distinguished Science Fellows program. Dr. Hill develops mathematical and computational tools to help better understand, predict, and treat infectious diseases, with a particular focus on human viral infections including HIV/AIDS. Hill received her PhD in 2013 through Harvard’s Biophysics Program and was a joint graduate student in the Harvard-MIT Division of Health-Sciences and Technology (HST)’s Medical Engineering and Medical Physics program. She received her undergraduate degree in Physics from Queen’s University in Ontario, Canada.
 Click here to view webcast.
Click here to view webcast.
Abstract
“Countdown to a Cure? Mathematical Approaches to Designing Better HIV Treatments”
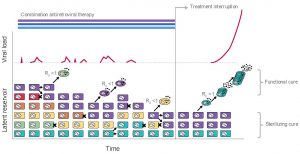 Individuals infected with HIV can now be prevented from progressing to AIDS, thanks to the introduction of combination antiretroviral therapy. However, these drugs are still unable to cure the infection, because long-lived latent virus persists despite years of treatment. If drugs are stopped at any point, the infection will quickly rebound, which makes global control of the epidemic extremely difficult. In this talk I will discuss how we use mathematical models of virus dynamics to evaluate new methods to cure HIV. First, I will show how these models have helped us understand how much the pool of latent virus must be reduced to delay or prevent the infection from rebounding when drugs are stopped. We explain why existing anti-latency drugs have had negligible benefit, and why we have seen multiple cases of apparent (but false) “cures” of HIV. We argue that math models should be used to help plan and interpret future clinical trials. Secondly, I will present a method to infer the mechanism of persistence of latent virus, based on the way the virus “tags” the cells it infects. We show that the natural proliferation of HIV-infected white blood cells drives virus persistence, and suggest that therapies to target this process could be highly effective. Overall, this work highlights the role that simulation, analysis, and inference using mathematical models can play in informing new potentially-curative treatments for HIV.
Individuals infected with HIV can now be prevented from progressing to AIDS, thanks to the introduction of combination antiretroviral therapy. However, these drugs are still unable to cure the infection, because long-lived latent virus persists despite years of treatment. If drugs are stopped at any point, the infection will quickly rebound, which makes global control of the epidemic extremely difficult. In this talk I will discuss how we use mathematical models of virus dynamics to evaluate new methods to cure HIV. First, I will show how these models have helped us understand how much the pool of latent virus must be reduced to delay or prevent the infection from rebounding when drugs are stopped. We explain why existing anti-latency drugs have had negligible benefit, and why we have seen multiple cases of apparent (but false) “cures” of HIV. We argue that math models should be used to help plan and interpret future clinical trials. Secondly, I will present a method to infer the mechanism of persistence of latent virus, based on the way the virus “tags” the cells it infects. We show that the natural proliferation of HIV-infected white blood cells drives virus persistence, and suggest that therapies to target this process could be highly effective. Overall, this work highlights the role that simulation, analysis, and inference using mathematical models can play in informing new potentially-curative treatments for HIV.
 Click here to view webcast.
Click here to view webcast.